COVID-19: Modeling Distributions of Incubation and Recovery Times
There is a flurry of models becoming available for the coronavirus pandemic we are in the midst of. We at isee systems have issued our own, available here. We’ve noticed a number of people use the canonical Susceptible-Exposed-Infected-Recovered (SEIR) model (in its simplest form):
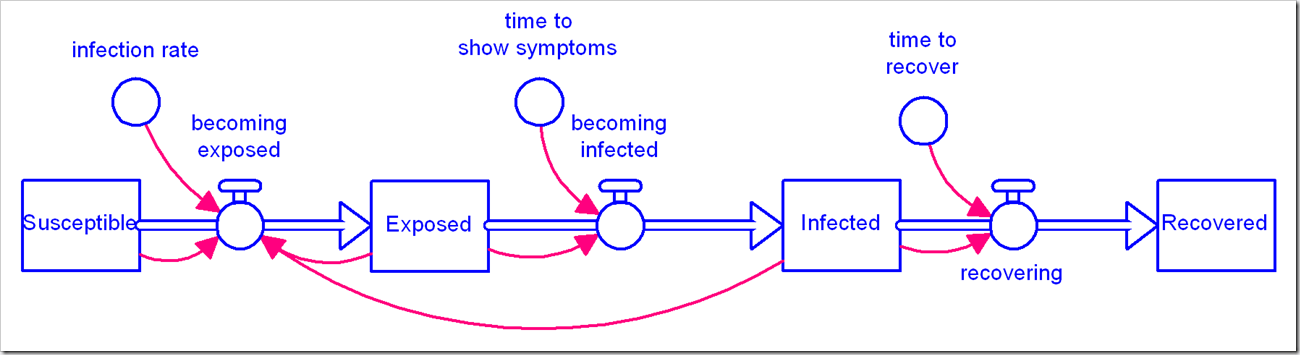 We’ve used this same model, albeit with disaggregation of severity of infection and the population that has been tested. We observed with our model that the simple first-order material delay used to model Exposed people becoming Infected and Infected people becoming Recovered is not appropriate for this situation and has a significant impact on the results. We chose to use an infinite-order delay, but that also is not quite right.
We’ve used this same model, albeit with disaggregation of severity of infection and the population that has been tested. We observed with our model that the simple first-order material delay used to model Exposed people becoming Infected and Infected people becoming Recovered is not appropriate for this situation and has a significant impact on the results. We chose to use an infinite-order delay, but that also is not quite right.
When choosing the order of a delay, one should consider the distribution of times around the specified delay time. An infinite-order delay will delay all material for exactly that amount. However, lower-order delays will delay material according to a distribution. The shape of that distribution can be discerned with a PULSE. As you can see in the graph below, the first-order material delay releases a large fraction of material almost immediately.
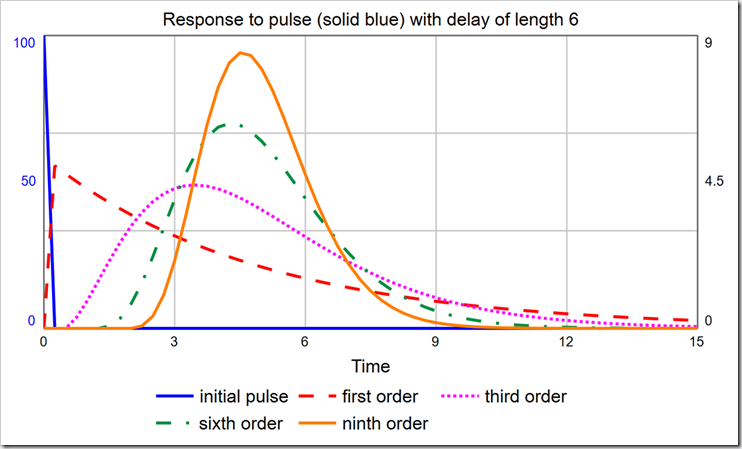 With a delay time of six, the modes for the 1st-, 3rd-, 6th-, and 9th-order delays are, respectively: DT (0.25), 3.5, 4.25, and 4.5. It is certainly not true that the largest group of people who become Exposed move on to being Infected almost immediately (after one DT). To correct this, we must use a higher-order material delay. Notice the 3rd-, 6th-, and 9th-order delays are all skewed right (their peaks are not centered on the actual delay value, which is six, and they are asymmetric). You can pick the order that most closely matches the actual distribution of, for example, time to show symptoms. The latest data I saw said that the average time to show symptoms is 5 days, but many cases can be 14 or more days. This indicates a long tail on the right side, making a 3rd- or a 6th-order more appropriate than a 9th-order. It would be ideal, though, if we could experiment with different distributions just by changing the order.
With a delay time of six, the modes for the 1st-, 3rd-, 6th-, and 9th-order delays are, respectively: DT (0.25), 3.5, 4.25, and 4.5. It is certainly not true that the largest group of people who become Exposed move on to being Infected almost immediately (after one DT). To correct this, we must use a higher-order material delay. Notice the 3rd-, 6th-, and 9th-order delays are all skewed right (their peaks are not centered on the actual delay value, which is six, and they are asymmetric). You can pick the order that most closely matches the actual distribution of, for example, time to show symptoms. The latest data I saw said that the average time to show symptoms is 5 days, but many cases can be 14 or more days. This indicates a long tail on the right side, making a 3rd- or a 6th-order more appropriate than a 9th-order. It would be ideal, though, if we could experiment with different distributions just by changing the order.
Normally, we would explicitly expand the model to handle a higher-order delay. However, consider that a 3rd-order delay requires three stocks, and a 6th-order requires six stocks, instead of just one. This muddies up the diagram quite a bit and does not give us the flexibility to easily change the order because any change requires a change to the model structure. The alternative is to use the DELAYN function, which allows you to specify the order of the delay as a parameter. The problem with this approach is that you only have access to the output of the delay (a flow); you no longer have access to the contents of the stock. In this application, we need to see how many people are Exposed and Infected. In Business Dynamics, John Sterman proposes the following structure for this exact circumstance:
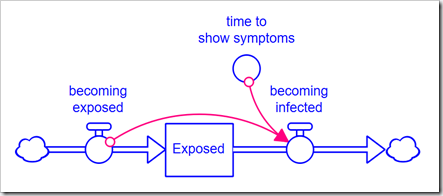 Rather than formulate the outflow becoming infected as a draining process (based on the stock), it is formulated from the inflow using the equation, for example, for a 3rd-order delay:
Rather than formulate the outflow becoming infected as a draining process (based on the stock), it is formulated from the inflow using the equation, for example, for a 3rd-order delay:
DELAY3(becoming_exposed, time_to_show_symptoms, 0)