Storytelling Simulations

Storytelling is a powerful feature that provides precise control over the presentation of a model to your audience. It also allows kiosk-style presentations to be created that step through the model, explaining it piece-by-piece. Many people use it only for this purpose, but storytelling offers so much more.

Because a basic premise of System Dynamics is that structure and behavior are linked, one of the key ideas behind storytelling is to allow the behavioral story to grow as the structural story unfurls. To create this effect, we neutralize structure that is not showing. This is extremely powerful because it allows you, for example, to selectively show the behavior of different loops within the system.

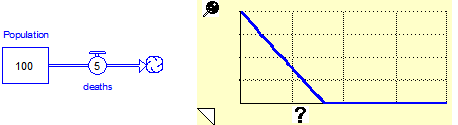
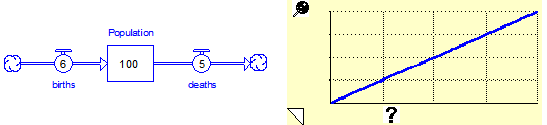
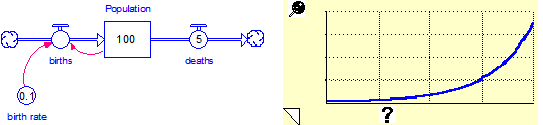
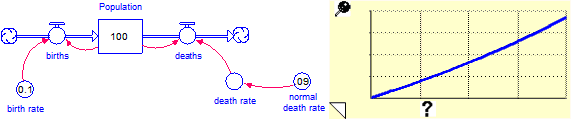
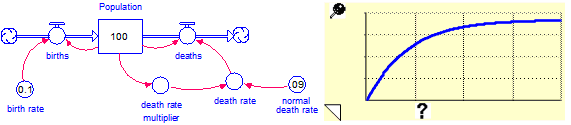
A simple example will solidify this concept. Consider the following simple population model:

The death rate multiplier is a simple resource constraint on the growth of population. More complex constraints would also affect the birth rate.

This model can be sequenced into a very meaningful structure/behavior story. The storyboard with the corresponding graph of Population for each story panel is:

death rate multiplier = Population/INIT(Population)

Note how the behavior of the model changes as more of the structure becomes extant, and especially as more loops are closed. This is something that cannot be done with, for example, Run by Modules or Run by Sectors.

How Run by Modules/Sectors Operates

These latter two run options work identically. When you run a set of modules (or sectors), inputs from modules that are not running are held at their initial values. Flows across the boundary act as if there is a cloud at whichever end is not in the running module. If sectors are placed around the different pieces of structure in this story and Run by Sectors is used, the behavior is identical (the second to last graph) for all steps but the last.

How Running Under Storytelling Operates

In storytelling, entities that are not visible are essentially removed from the model. The program neutralizes them by setting them to either zero or one based on how they are used in each visible entity’s equation. If there is a either a “+” or a “-” in the visible entity’s equation, the invisible entity will evaluate to zero in that equation. Otherwise, it will evaluate to one in that equation. You can override this default behavior for each entity in the storytelling dialog. In addition, flows that have none of their inputs shown can also be set to default values by hovering over them and typing in a value. This is how births and deaths were set in the first two panels of the story.

Let’s look at a few simple examples to get the feel of it. Let a = 5, b = 7, and c = 2.

The story panels below show the values of x under these scenarios of visible and invisible entities.

x = a + b:

The equation is additive, therefore entities not shown are set equal to 0

Visible Entities
Values	a = 0, b = 0	a = 5, b = 0	a = 0, b = 7	a = 5, b = 7
x	0 + 0 = 0	5 + 0 = 5	0 + 7 = 7	5 + 7 = 12

x = a*b:

The equation is multiplicative, therefore entities not shown are set equal to 1

Visible Entities
Values	a = 1, b = 1	a = 5, b = 1	a = 1, b = 7	a = 5, b = 7
x	1*1 = 1	5*1 = 5	1*7 = 7	5*7 = 35

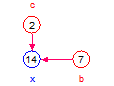
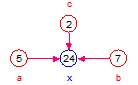
x = (a + b)*c:

The equation is treated as additive because it has a + symbol, therefore entities not shown are set equal to 0

Visible Entities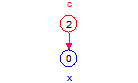
Values	a = 0, b = 0, c = 0	a = 5, b = 0, c = 0	a = 0, b = 7, c = 0	a = 0, b = 0, c = 2
x	(0 + 0)*0 = 0	(5 + 0)*0 = 0	(0 + 7)*0 = 0	(0 + 0)*2 = 0

Visible Entities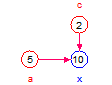
Values	a = 5, b = 7, c = 0	a = 5, b = 0, c = 2	a = 0, b = 7, c = 2	a = 5, b = 7, c = 2
x	(5 + 7)*0 = 0	(5 + 0)*2 = 10	(0 + 7)*2 = 14	(5 + 7)*2 = 24

The value of the invisible variables is zero in the first and last cases, and one in the middle case. The last case is treated as additive by default because there is a plus sign. This may or may not give the result desired.

It is possible to override the default behavior in the storytelling dialog (by selecting the entity and using the “+ -> *” button at the bottom), though this may not be desired depending on the application. However, to ensure the desired result by default, separate such expressions into their additive and multiplicative components. In this case, add a converter d = a + b and make x = d*c. In this way, x will only be zero when both a and b are invisible.

The following story panels show the values of x under these scenarios of visible and invisible entities.

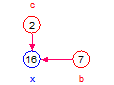
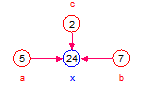
x = (a + b)*c overridden to be multiplicative:

The default additive behavior is overridden to be multiplicative in this case and therefore the entities not shown are set equal to 1

Visible Entities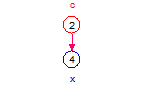
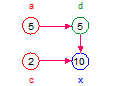
Values	a = 1, b = 1, c = 1	a = 5, b = 1, c = 1	a = 1, b = 7, c = 1	a = 1, b = 1, c = 2
x	(1 + 1)*1 = 1	(5 + 1)*1 = 6	(1 + 7)*1 = 8	(1 + 1)*2 = 4

Visible Entities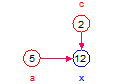
Values	a = 5, b = 7, c = 1	a = 5, b = 1, c = 2	a = 1, b = 7, c = 2	a = 5, b = 7, c = 2
x	(5 + 7)*1 = 12	(5 + 1)*2 = 12	(1 + 7)*2 = 16	(5 + 7)*2 = 24

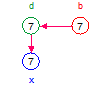
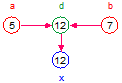
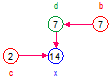
x = d*c, where d = a + b:

The equation behavior for x is multiplicative and for d it is additive. Entities that are not shown and inputs to x will be set equal to 1. Entities that are not shown and inputs to d will be set equal to 0.

Visible Entities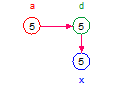
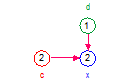
Values	d = 1, c = 1	d = 1, c = 2	a = 5, b = 0, c = 1	a = 0, b = 7, c = 1	d = 1, c = 2
x	1*1 = 1	1*2 = 2	(5 + 0)*1 = 5	(0 + 7)*1 = 7	1*2 = 2
Note	a and b are not evaluated	a and b are not evaluated			a and b are not evaluated

Visible Entities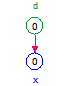
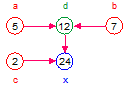Values	d = 0, c = 1	a = 5, b = 7, c = 1	a = 5, b = 0, c = 2	a = 0, b = 7, c = 2	a = 5, b = 7, c = 2
x	0*1 = 0	(5 + 7)*1 = 12	(5 + 0)*2 = 10	(0 + 7)*2 = 14	(5 + 7)*2 = 24
Note	a and b are not evaluated

Behavior of Ghosts Under Storytelling

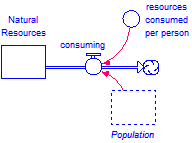
Finally, ghosts behave the same, irrespective of whether their parent is visible. This means all the above rules apply, which can sometimes be confusing. For example, if a stock called Population initialized to the constant 100, the story below does what is expected: the ghost of Population will equal 100.

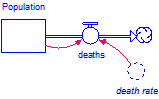
However, in the story below, the behavior is not very likely to be what is expected. If death rate is a constant, there will be no surprises. However, if death rate depends on other variables, as in the example at the beginning of this post, you may be very surprised by the results. In that case, death rate was determined by multiplying two other variables, so it will evaluate to one in this story. To make it evaluate to a more meaningful value, you must also include some of its inputs in this story panel (as was done in that story). This is true, by the way, whether death rate is a ghost or not.

The simulation rules for storytelling can sometimes lead to confusing results, especially in larger models. Hopefully, this post clears up much of the confusion and allows you to build more effective behavioral stories.