Methods for Using Arrays Effectively, Part 1
This is the first installment of a four-part series. The remaining three parts can be accessed by clicking on the links below.
Modeling a Watershed with Arrays
Modeling Customers Switching Between Brands
Modeling Customers Switching Between Brands – The General Case
Using arrays can be quite intimidating for most people. Many times, it is difficult to discover the correct way to formulate a problem in terms of arrays, especially when trying to do so in terms of single equations that can be applied to all elements of the array.
Consider the case where you might wish to count the number of occurrences of a value in an array. This can arise in many applications that need to track attributes, but is prevalent in spatially-explicit business applications. In such an application, you may associate a product code with a location and then want a count of the products of a given type. The following examples demonstrate a common way to extract conditional information from an array.
Finding the Number of Stations with a Given Status
Imagine you have a two-dimensional grid of fire stations in a city, called Stations, that stores one of four statuses:
0: no station in this sector
1: ready
2: away on a call
3: refitting
You consider the number of fire stations ready at any given moment to be an important metric. To calculate this, connect Stations to another two-dimensional array of the same size called ready stations. This will have a one in an array element if the station for that quadrant is ready and a zero otherwise. Its equation is:
IF Stations[Y, X] = 1 THEN 1 ELSE 0 { station ready? }
Note this equations uses dimension names (i.e., Stations[Y, X]) rather than element names (e.g., Stations[1, 2]). This allows you to create just one equation for the entire array (with “Apply to All” turned on), rather than a separate equation for each individual array element (with “Apply to All” turned off). When “Apply to All” is turned on, the equation for each element of the array is automatically generated by substituting that element’s dimensions for the dimension name in the given equation. All of the examples in this post use dimension names.
The total number of ready stations is now just the sum of all of the elements in the array ready stations. This is easily calculated by connecting ready stations to a scalar converter named total ready stations that has the equation
ARRAYSUM(ready_stations[*, *])
The model is shown below and can be downloaded by clicking here.
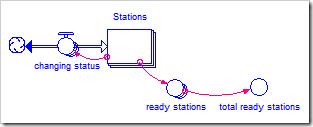
This general method can be used anytime we need to count the number of elements in an array based on some condition. First, create an array that has its elements set to one if the array-based condition is met and zero otherwise (IF condition THEN 1 ELSE 0). Then create a converter to sum the elements of this new array (using ARRAYSUM). Remember to turn “Apply to All” on and use dimension names in the condition rather than element names.
Finding the Number of Stations with Each Status
We can extend this method to map data from an array indexed by one attribute (or dimension), say location, to another array indexed by a different attribute, say status. Imagine now that instead of just counting how many stations are ready, you want to know how many stations have each status.
One way to do this is to extend the structure above to separately count the number of stations in each status, as shown below.
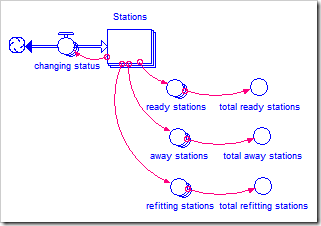
In this case, away stations and refitting stations have the following formulas, respectively:
IF Stations[Y, X] = 2 THEN 1 ELSE 0 { station away? }
IF Stations[Y, X] = 3 THEN 1 ELSE 0 { station refitting? }
Walking Through a Specific Example
Let’s look at what happens in this model if array of fire stations is only one-dimensional, Stations[Location], and each location is named. This eliminates the “no station in this sector” status. Consider a five-location fire department with the following statuses in each location, held in the array Stations:
| Location | Status |
| North | 1 (ready) |
| South | 3 (refitting) |
| Central | 1 (ready) |
| East | 2 (away) |
| West | 1 (ready) |
The structure above would generate the following values in the three separate arrays ready stations, away stations, and refitting stations. Their respective sums, in the three corresponding “total status stations” converters, are shown at the bottom.
| Location | ready stations |
away stations |
refitting stations |
| North | 1 | 0 | 0 |
| South | 0 | 0 | 1 |
| Central | 1 | 0 | 0 |
| East | 0 | 1 | 0 |
| West | 1 | 0 | 0 |
| total status stations | 3 | 1 | 1 |
While this method works, it does not have a very flexible structure. It requires structural changes whenever a new status is added (or removed) and also needs to be customized for every individual application. There are also applications (for example, tracking products) where it is necessary to move between arrays that are indexed by location, as Stations is, and arrays that are indexed by the data within the location, in this case by status.
A More General Solution
If we define another array dimension called Status, with element names Ready, Away, and Refitting that correspond to the numeric statuses 1, 2, and 3, we can represent this same solution in one two-dimensional array station map[Location, Status]:
| Location | Ready | Away | Refitting |
| North | 1 | 0 | 0 |
| South | 0 | 0 | 1 |
| Central | 1 | 0 | 0 |
| East | 0 | 1 | 0 |
| West | 1 | 0 | 0 |
The array station map allows us to map stations directly to their statuses. Each row of the map represents one station. By definition, there can only be one “1” in each row because a station can only have one status. The sum of each row is the number of statuses that are assigned to that station, which must always be one. Each column of the map represents one status. Multiple “1”s can appear in the columns because many stations can have the same status. The sum of each column is the number of stations assigned to that status, the value we are trying to determine.
Note the similarity between this two-dimensional array and the preceding table that shows the contents of the individual one-dimensional arrays ready stations, away stations, and refitting stations. Each column of station map corresponds to one of these one-dimensional arrays.
The model for this more general solution is shown below and can be downloaded by clicking here.
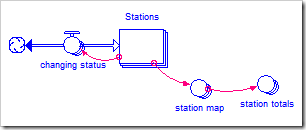
The equation for station map[Location, Status], which will map Stations as illustrated above, is
IF Stations[Location] = ARRAYIDX(2) THEN 1 ELSE 0
Note the use of ARRAYIDX() to parameterize the status we are interested in for this array element. The parameter to ARRAYIDX, 2, gives the index of the second dimension for this array element, i.e., the index that corresponds to Status. Since Apply to All is on, this will become the desired status for each array element.
The number of stations with each status is calculated in the one-dimensional converter station totals[Status] using the equation
ARRAYSUM(station_map[*, Status])
This equation sums the columns of station map. For the above example, station totals will be filled with the values 3 (Ready), 1 (Away), and 1 (Refitting). Note we have used an intermediate two-dimensional array, station map, to properly map our data from a one-dimensional array indexed by the attribute Location to another one-dimensional array indexed by the attribute Status.
Next time, I will expand this concept to create general routing structures.