Modeling Customers Switching Between Brands
This is the third installment of a four-part series. The other three parts can be accessed by clicking on the links below.
Methods for Using Arrays Effectively
Modeling a Watershed with Arrays
Modeling Customers Switching Between Brands – The General Case
In the second post of this series, I showed how to selectively pull information from an array in order to route water through a watershed. In this post, I will use the exact same technique to move customers between different product brands.
Switching Customers between Different Products
Business models often need to model gaining customers from, and losing customers to, competing products in a relatively mature market (what Kim Warren, in his excellent book Strategy Management Dynamics, calls “Type 2 Rivalry”). These are often driven with statistical models developed through market research. For this application, we need a matrix describing the probability of switching from product A to product B each time unit. A sample appears in the table below.
| From\To | A | B | C | D | E |
| A | 0.000 | 0.010 | 0.030 | 0.050 | 0.001 |
| B | 0.030 | 0.000 | 0.050 | 0.070 | 0.020 |
| C | 0.010 | 0.001 | 0.000 | 0.020 | 0.015 |
| D | 0.001 | 0.000 | 0.020 | 0.000 | 0.005 |
| E | 0.001 | 0.005 | 0.020 | 0.045 | 0.000 |
switching probability (units: dimensionless)
To read this table, locate the product the customer is presently using in the left column (say, B). Read across that row (the second row, in this case) until you find the product the customer is switching to (say, C). The number in that cell (in this case, 0.05 or 5%) is the probability the customer will switch from the first product to the second (from B to C) in this time unit. If the model is running in months, as ours is, this table indicates that 5% of customers using product B switch to product C every month.
Of course, the values in the table do not need to be constant. Often each cell will contain a regression equation based on various product characteristics – including market share, marketing effort, product features, and product quality – that evolve over the course of the simulation.
Note the diagonal is zero. This means customers do not switch from one product to the same product.
Note also that the sum in any row cannot exceed 1.0, which represents 100% of the customers using that product. It is quite normal for it to be below 1.0 because we do not include people who are not switching. Some modelers find it easier to always have each row add up to 1.0. If you desire to do this, fill the diagonal with the difference between 1.0 and the sum of the other columns. For example, to do this for product A, replace the top left cell with 1.0 – (0.01 + 0.03 + 0.05 + 0.001) = 0.909 [for you Beatles fans].
Exploring the Model
The model is slightly different from the watershed model in my previous post. This model is driven by the probability of switching. Thus, it is driven by the stock of customers for each product, while the watershed model was driven by the outflow from each reach. This is shown below (and is available by clicking here).
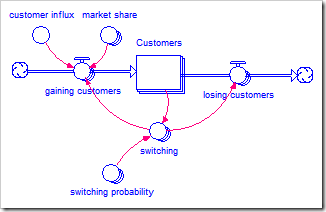
The two-dimensional array switching (called a “switching matrix”) is derived by multiplying customers by the switching probability:
Customers[Products]*switching_probability[Products, Products]
This equation does not perform a traditional matrix multiplication, but multiplies each element of Customers (a one-dimensional column) by every element in the corresponding row of switching probability (two-dimensional). [For more information about matrix arithmetic in iThink and STELLA, click here.] As an example, given the switching probability above, if 100 customers use each of products A, B, C, D, and E, the values of switching with its row and column totals would be:
| From\To | A | B | C | D | E | Total Out |
| A | 0.0 | 1.0 | 3.0 | 5.0 | 0.1 | 9.1 |
| B | 3.0 | 0.0 | 5.0 | 7.0 | 2.0 | 17.0 |
| C | 1.0 | 0.1 | 0.0 | 2.0 | 1.5 | 4.6 |
| D | 0.1 | 0.0 | 2.0 | 0.0 | 0.5 | 2.6 |
| E | 0.1 | 0.5 | 2.0 | 4.5 | 0.0 | 7.1 |
| Total In | 4.2 | 1.6 | 12.0 | 18.5 | 4.1 | 40.4 |
switching (units: customers)
These numbers are derived by multiplying the entire row for each product by 100, the number of customers using that product (again, this example uses 100 customers for each product). The number of customers switching from a given brand each month is the sum of that product’s row. The number of customers switching to a given brand each month is the sum of that product’s column.
Thus, 9.1 existing customers switch from (stop using) product A this month while 4.2 customers switch to (start using) product A this month. Product A will therefore have a net loss of 9.1 – 4.2 = 4.9 customers for the month.
The switching matrix directly drives both the loss of customers and the gain of customers. The former, losing_customers, sums rows:
ARRAYSUM(switching[Products, *])
while the latter, gaining_customers, sums columns:
ARRAYSUM(switching[*, Products]).
Running the Model
The simulation results are shown below for the case where all products start with 100 customers and no new customers are added.
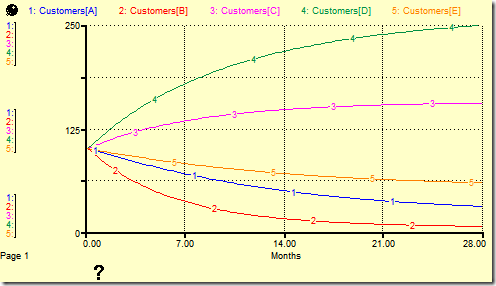
Note the product with the largest net gain = Total In – Total Out, product D, gains the most market share over the course of the simulation, while that with the smallest net gain, product B, loses the most.
Next time, I will show a more general switching matrix formulation.