Limits to Growth

This is the first of a three-part series on the Limits to Growth Archetype.  The second part can be accessed here and the third part here.

The Limits to Growth Systems Archetype, also known as Limits to Success, combines growth with an exogenous or endogenous limit.  This Systems Archetype was formally identified in Appendix 2 of The Fifth Discipline by Peter Senge (1990), but made its first prominent appearance in World Dynamics by Jay Forrester (1971) and then The Limits to Growth by Meadows, Meadows, Randers, and Behrens (1972).  The Causal Loop Diagram (CLD) is shown below.

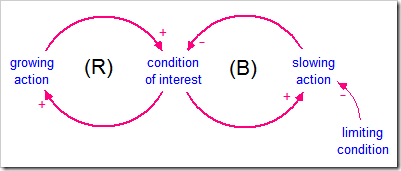
Real growth processes have inherent limits to growth.  Identifying these limits can help avoid problems in the future, whether the problem is overpopulation, increasing demand for a product that cannot be met, or growing a business in a mature market.  When growth is desired, but limited, it is always better to find ways to increase the limit before pushing for more growth.  Excessive growth in the face of a limit often leads to collapse.  Driving the system to the point of collapse can erode the ability to continue after the collapse, for example, by reducing the production capability of a piece of farmland or destroying the reputation of a company.

Classic examples of limits to growth include:

• The collapse of the deer population on the Kaibab plateau and on St. Matthew Island due to overpopulation and the attendant overgrazing of their habitat
• The overshoot and collapse of the human population on Easter Island
• Overgrazing in the Sahel region of Africa by cattle herders
• Overfishing of the oceans by fishermen
• The collapse of People Express due to sharp customer growth combined with slow personnel growth
• The sharp exodus of America Online subscribers after an intense marketing campaign increased the number of subscribers far beyond their capacity
• The contraction of the world economy in 2008 due to limiting oil supplies
• The productivity of staff deteriorating as a company grows, due to increased interactions and reporting overhead
• Business growth limited by the size of the potential market
• Yeast cells in the fermentation process, who suffer from both the loss of exogenously supplied sugar and the increase of endogenously produced pollution

Exploring Limits to Growth with the SIR Model

The SIR (Susceptible-Infected-Recovered) model, also known as the Kermack-McKendrick model, is used to predict the spread of an infectious disease.  The disease is ultimately limited by the number of potential hosts.

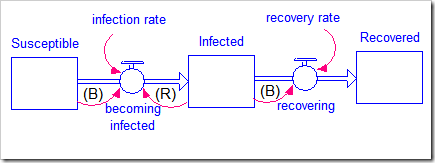
In this model (available by clicking here), the Susceptible population becomes infected based on their rate of contact with an Infected population and the probability of being infected (infection rate combines these parameters).  After some amount of time (1/recovery rate), the disease runs its course and people either recover or die, moving into the Recovered population.

The infection feeds on susceptible people.  As the number of susceptible people falls, the number who can become infected also falls.  Since infected people eventually recover, the number of infected people will ultimately fall.  This behavior is reflected in the graph below.

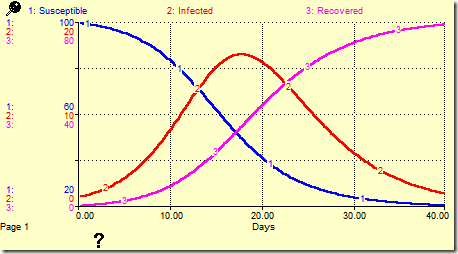
The sharp increase in Infected, followed by a dramatic drop is known as overshoot and collapse.  It is a characteristic behavior of the Limits to Growth Archetype.  The stock of Recovered people is also limited – by the total population.  It exhibits a different characteristic behavior of Limits to Growth:  S-shaped growth, so called because the graph of this growth pattern looks like the letter S.  This is also known as logistic growth.  In the beginning, growth is very rapid, but as the limit is approached, growth slows and then stops.  In feedback terms (refer back to the CLD), the rapid growth on the left side of the S occurs because the reinforcing loop dominates while the right side slowdown occurs because the balancing loop dominates.

There are two separate limits to growth:  one on the sustainable level of the condition of interest and one on its rate of growth.  The former is defined by a system’s carrying capacity (named limiting condition in the CLD).  As Khalid Saeed, Professor of Social Science and Policy Studies at Worcestor Polytechnic Institute, recently reminded me, the carrying capacity of a system is always a flow.  Any system that requires something, either energy or mass, to persist cannot exist beyond the level at which that something can be provided.  The second limit, that on the rate of growth, is defined by the system slack, which is always a stock.

In the SIR model, the infectious disease feeds off of the susceptible people.  The stock of Susceptible people is therefore the slack in the system.  The growth of the disease is limited by the contents of this stock.  However, the carrying capacity of the system is zero, as there is no inflow to Susceptible to provide an endless supply of victims for the disease.  The net result is that eventually, and after a sharp rate of growth, the number of infected people will also drop to zero.

In either a closed or a quarantined community, this may be true.  However, ease of travel creates an inflow to Susceptible, i.e., a carrying capacity, and thus the disease can persist.  The graph below shows what happens when an inflow is added Susceptible and set to 10 people per day (10% of the initial population).

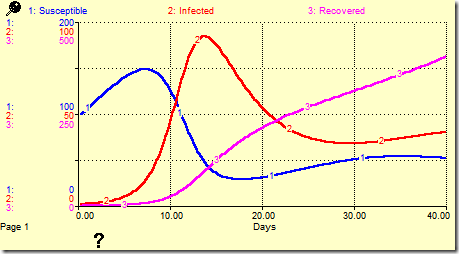
Rather than going to zero, both Susceptible and Infected wind up at non-zero steady-state values that reflect the new carrying capacity (10).  Note in particular that this value is not 10 for either stock; it is about 50.  Note also that the Infected peak has risen from roughly 17 to 90 due to the inflow of susceptible people.

For more information about the spread of infectious disease, read our blog post on Modeling H1N1 Flu Outbreak.

Exploring Limits to Growth in Population Dynamics

Another example occurs in population dynamics.  The simple example shown below demonstrates the impact of a limit (click here to download this model).

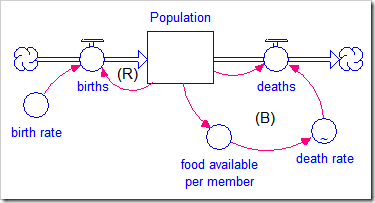
The food available is a simple linear relationship that reduces available food as population increases.  The death rate increases as the available food per member of the population falls.  The behavior of this model is shown below.

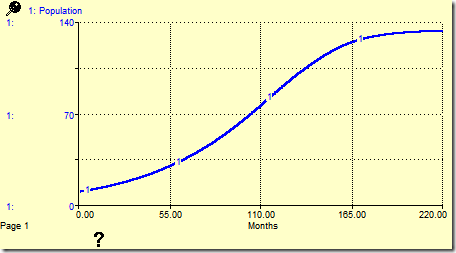
While this shows the desired behavior, an exogenous limit (food available) enforced as the population grows, this model has no slack and no explicit carrying capacity.  The lack of an explicit stock to model the slack in the system will result in an incorrect transient response (i.e., the system’s response to a change in its variables) when something happens that might require that slack, for example, a drought or a surge in the population due to immigration.

A more accurate and useful, though more complex, model appears below (and is available by clicking here).

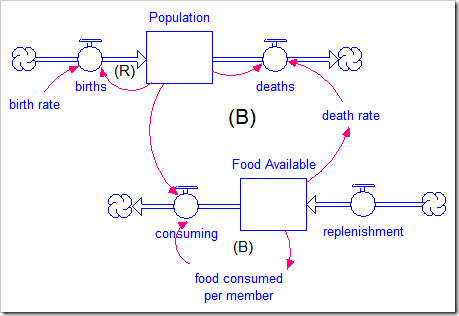
Both the carrying capacity (replenishment) and the slack (Food Available) are explicitly modeled.  The behavior is quite different:

 

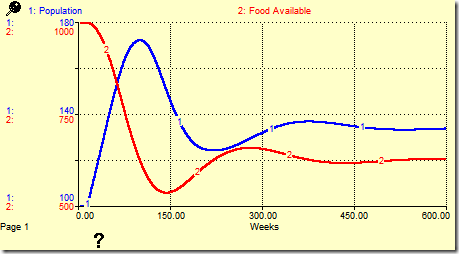
There is now a proper transient response to an increase in the birth rate.  The slack, Food Available, fuels growth in the Population until the slack is exhausted (relative to the carrying capacity), at which point the population collapses to its approximate equilibrium value – the value supported by the carrying capacity.

Next time, I will explore limits to growth in the context of business development models.